Compact Lexer Table Representation
2020-05-02 15:31:09+02:00
I found surprisingly little information on the transition table of a lexer generator.
There are plenty of resources on the front-end, such as the very nice Regular-expression derivatives reexamined paper.
However, resources on the transition table are much more scarce. Eventually, I found two references: The Dragon Book, which explains a clever scheme for packing the table, and OCamllex which implements it[^fn1].
Update: Software and Hardware Techniques for Efficient Polymorphic Calls thesis analyzes a variant of the technique described in this post to store dispatch tables of object-oriented tables. "Row displacement" proves to be very efficient in a closed world and extends well to multiple inheritance.
[^fn1]: Actually, I believe that the pseudo-code in The Dragon Book is wrong. There should be no recursive call to nextState, instead the default state should be returned directly. This is what OCamllex does.
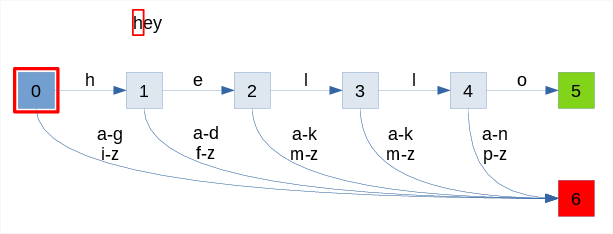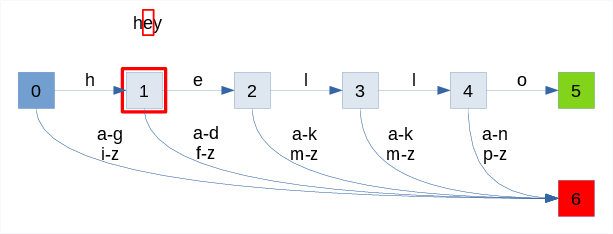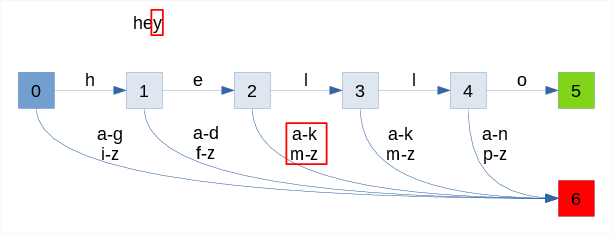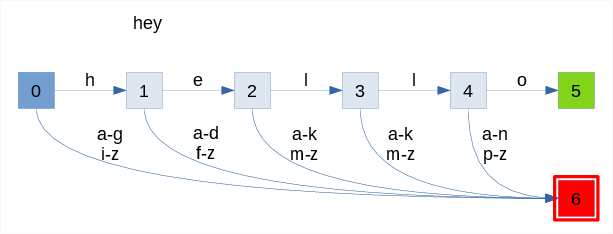
The Transition Table
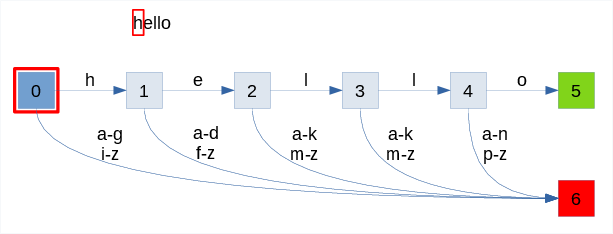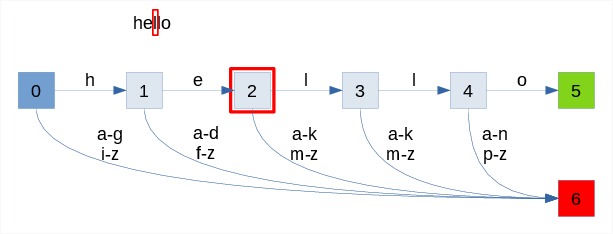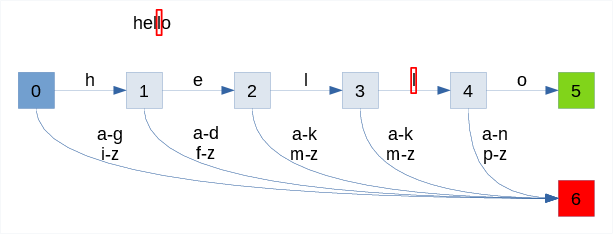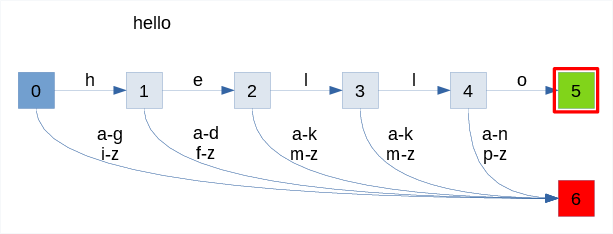
The lexer generator frontend produces a deterministic finite automaton (DFA). Transitions are labeled by symbols from the input alphabet (a-z characters in the illustration below). Here is a trivial DFA recognizing the word "hello":
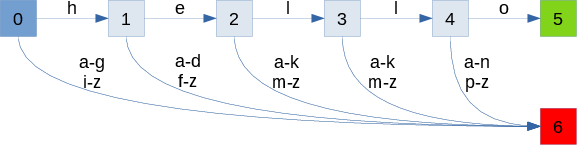
We start from state 0 (the initial state). Then we follow the transitions until:
- acceptance: if we reach state 5, the word "hello" has been recognized
- rejection: if we reach state 6, recognition failed
The animation below shows the process of recognizing two words:
- success with "hello" input
- failure with "hey"
We need an efficient way to store and follow these transitions.
Naive Representation
The simplest representation is a matrix indexed by states and characters. In C, that looks like:
// state_t is the type representing a state
// 256 because we work with 8-bit characters
state_t transition_table[MAX_STATES][256];
state_t next_state(state_t current, uint8_t input)
{
return transition_table[current][input];
}
This is efficient in time but not in space. The difficulty lies in finding a compact representation that does not compromise speed:
- Transitions will be followed for every input byte. This is the hottest part of the lexing process.
- Practical languages can grow to thousands of states. The matrix takes a few megabytes of memory.
Here is the matrix for the "hello" example:
| \ | a...d | e | f,g | h | i,j,k | l | m,n | o | p...z |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 6 | 6 | 1 | 6 | 6 | 6 | 6 | 6 |
| 1 | 6 | 2 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 2 | 6 | 6 | 6 | 6 | 6 | 3 | 6 | 6 | 6 |
| 3 | 6 | 6 | 6 | 6 | 6 | 4 | 6 | 6 | 6 |
| 4 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 6 |
We can see that it is very explicit and very redundant. A transition is very likely to be 6!
Sparse representation
The Dragon Book suggests representing each transition vector (a row of the table above) sparsely:
- default transition: remember the most common target destination
- non-default transitions: store only the transitions that differ
With associative lists
The sparse vectors can be represented with a default value and an associative list for storing non-default transitions.
The table becomes:
| default | Transitions | |
|---|---|---|
| 0 | 6 | (h, 1) |
| 1 | 6 | (e, 2) |
| 2 | 6 | (l, 3) |
| 3 | 6 | (l, 4) |
| 4 | 6 | (o, 5) |
Much more compact!
But there is a performance problem: for each transition, we have to iterate the list looking for a match. A list can be as big as the size of the alphabet. That would lead to unpredictable and often slow performance – unacceptable.
With overlapping vectors
The Dragon Book comes to the rescue and introduces a clever scheme that retains the performance of array-based lookup with the compactness of sparse vectors. The scheme is as follows:
- Store all vectors in the same array
- Offset them such that only non-default transitions don't overlap
- Annotate the non-default transitions with their source state
With this mechanism, the automaton looks like:
State table:
Default Offset 0 6 0 1 6 0 2 6 0 3 6 1 4 6 0 Transition table:
index 0...3 4 5,6 7 8,9,10 11 12 13 14 15..26 source Ø 1 Ø 0 Ø 2 3 Ø 4 Ø target Ø 2 Ø 1 Ø 3 4 Ø 5 Ø (Using Ø: any value that does not represent a valid state)
We avoid the waste of the naive matrix by filling the unused cells of sparse vectors with the content of others. And we keep the fast access characteristics of arrays.
Here is the mapping between index and characters at offset 0 and 1:
| index | 0 | 1,2,3 | 4 | 5,6 | 7 | 8,9,10 | 11 | 12 | 13 | 14 | 15..25 | 26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| at offset 0 | a | b,c,d | e | f,g | h | i,j,k | l | m | n | o | p..z | |
| at offset 1 | a,b,c | d | e,f | g | h,i,j | k | l | m | n | o..w | z |
States 0, 1, 2, and 4, have been given the offset 0. Their non-default transitions never conflict: rather than having a separate vector of 26-elements for each of them, we can overlap all of them in the same vector.
State 3 is more complicated. It cannot be at offset 0: it has a transition on l that would end up at column 11. But this column is already used by state 2. However the column 12, just after, is not used by other states. So we offset the state by 1, shifting the meaning of characters: l at offset 1 maps to column 12. (It coincides with m at offset 0, but no state has a transition on m.)
With offsets, all transitions can fit in a single vector of 27 elements. Each cell is a bit larger because it stores a pair of states (a source and a target).
The implementation is now:
typedef struct {
state_t default_;
int offset;
} state_desc;
typedef struct {
state_t source, target;
} transition_t;
state_desc state_table[MAX_STATES];
transition_t transition_table[MAX_TRANSITIONS];
state_t next_state(state_t current, uint8_t input)
{
int index = state_table[current].offset + input;
if (transition_table[index].source == current)
return transition_table[index].target;
else
return state_table[current].default_;
}
The tables are a bit harder to generate than the naive matrix. How do we find the right offsets? A simple greedy strategy gives good packings:
- Start from first vector
- Try to fit it at offset 0:
- If there is no overlap, done
- If it overlaps, try again at the next offset
- Repeat with the next vector, until all vectors are packed
Engineering tricks
Algorithmically, this solution is satisfying. I went a bit further to make it more hardware friendly while maintaining a good space/time trade-off.
Something we did not specify above is the size of each type. How many bits for a state_t? OCamllex has hard-coded limits that can be reached on big yet realistic languages. These limits save space but make the lexer less flexible. I wanted more freedom here.
I set myself the goal of storing everything in a single array of 32-bits value. I ended up with 23 bits for offsets. This allows for a theoretical maximum of ~8 million transitions, using up to 32 MiB.
1. Disambiguate using characters
Rather than storing a source state in a transition to distinguish non-default from default transitions, store an input character: this transition is non-default if we reached it by following this input character. I call it the input disambiguator.
typedef struct {
uint8_t input;
state_t target;
} transition_t;
state_t next_state(state_t current, uint8_t input)
{
int index = state_table[current].offset + input;
if (transition_table[index].input == input)
return transition_table[index].target;
else
return state_table[current].default_;
}
This change alone removes just a few bits of information from a transition cell. And it forces us to store each state at a different offset (otherwise it would be ambiguous). For the "hello" example, offsets are now (0,1,2,3,4).
But we replaced a vector of states by a vector of characters. There can be many states but there are only 256 characters. We can exploit this in the low-level representation.
2. Represent states by their offsets
Now that each state has a unique offset we can directly represent them using offsets, rather than consecutive numbers.
We get rid of the offset entry from the state table and store the default_ transition as if it was on character "-1". Just before the offset:
transition_table[offset + c]: transition information from stateoffsetand input characterctransition_table[offset - 1]: default transition for stateoffset
The input disambiguator for transition_table[offset - 1] is chosen to not coincide with the non-default transition of another valid state. In other words offset - 1 - transition_table[offset - 1].input should not be the offset of another state.
Everything fits in a single array now:
typedef struct {
uint8_t input;
state_t target;
} transition_t;
transition_t transition_table[MAX_TRANSITIONS];
state_t next_state(state_t current, uint8_t input)
{
if (transition_table[current + input].input == input)
return transition_table[current + input].target;
else
return transition_table[current - 1].target;
}
By making the state fit in 24-bits, we can represent a transition in a single 32-bit value:
typedef int32_t state_t;
typedef struct {
uint8_t input : 8;
state_t target : 24;
} transition_t;
3. Negative numbers for special actions
In the example, states 5 and 6 have a special meaning: accepting or rejecting the input. From the point of view of the automaton they do the same: terminate the analysis and yield control back to the caller. It is the caller that will act differently based on the reason for the termination.
Thus the automaton does not assign any meaning to special transitions other than stopping the analysis. The driver, on the other hand, can have many actions. For instance:
- backtracking: remember the current state, continue the analysis and if it reaches a rejection state later, fall back to current state and act as if it was accepting
- tagging: mark the current state as a "point of interest" for the program, and resume the analysis. This can be used to implement capture groups
The special transitions just need to be distinguished from normal states. For this, I simply chose to use negative values, which cannot represent states. This reduces the amount of usable bits in a state_t to 23 (for a maximum table size of 32 MiB).
Handling end-of-file
End-of-file condition (EOF) is reached when there is no more input to feed to the automaton. That can happen at any time, we should always be ready to handle EOF.
Special actions behave like extra states, EOF behaves like an extra transition.
OCamllex deals with EOF regularly, by using an alphabet with 257 symbols. I chose to treat EOF differently:
- To keep using 8-bit integers for "input" disambiguator
- EOF is a unique situation, it happens only once per run and it happens last. It does not have to be on the fast path.
The remaining degree of freedom we had in the representation of states is the input disambiguator. We use it to encode EOF transition.
We will it to point to any unused transition cell that is now re-purposed to indicate the EOF destination state. The disambiguator of this EOF cell can be anything as long as it is not ambiguous. We end up with a different transition function for EOF:
state_t eof_state(state_t current)
{
int idx = transition_table[current - 1].input;
return transition_table[current - 1 - idx].target;
}
All these optimizations put more pressure on the packing algorithm. But the added freedom can reduce fragmentation in the sparse array, and in practice many states have the same EOF transition:
- The packing algorithm can share a single EOF cell with many states, improving efficiency.
- The original scheme, the one with many tables, have to give different offsets to each state. What seemed at first a drawback of the single table scheme also happens in the original one in practice.
There is a last optimization we can do for storing EOF transition. Because EOF happens at the end of the analysis, it only makes sense for EOF transitions to target special actions.
Therefore we can use this extra bit of information to introduce more sharing on EOF transitions. We can interpret EOF transitions targeting a regular state as a default transition. And then repeat looking for an EOF transition from this default state.
state_t eof_state(state_t current)
{
while (1)
{
int offset = transition_table[current - 1].input;
int eof_index = current - 1 - offset;
state_t target = transition_table[eof_index].target;
if (target <= 0)
return target;
current = transition_table[current - 1].target;
}
}
This complicates the packing scheme for diminishing returns. I did not bother implementing it.
Final implementation
Putting everything together, I got this implementation for the core loop of the lexer:
typedef int32_t state_t;
typedef uint32_t transition_t;
#define SRC(transition) ((transition) & 0xFF)
#define DST(transition) ((int32_t)(transition) >> 8)
state_t follow(transition_t *table, state_t state,
unsigned char **buf, unsigned char *end)
{
unsigned char *ptr = *buf;
while (ptr < end && state > 0)
{
unsigned char c = *ptr++;
transition_t def = table[state - 1];
transition_t nxt = table[state + c];
state = DST((SRC(nxt) == c) ? nxt : def);
}
*buf = ptr;
return state;
}
state_t follow_eof(transition_t *table, state_t state)
{
int idx = SRC(transition_table[state - 1]);
return DST(transition_table[state - 1 - idx]);
}
The interpretation function consume as many characters as possible. This reduces the interpretation overhead (the cost of entering and leaving the interpretation function). We want to spend most of the time in the hot loop!
Note that the loop is quite machine-friendly:
- The two loads can be issued in parallel
- State selection compiles to branch-less code
The only branching is the check for the exit condition. It is unavoidable but it happens once and is well predicted.
Conclusion
I presented some techniques for storing the transition table of a lexer. The main result is a simple 40-year-old scheme. It is effective and a few adjustments make it perform even better on modern hardware.
I apologize for not having benchmark figures to show... I did not want to spend the time implementing a production grade lexing engine. I was just interested in playing around the full pipeline rather than stopping after the frontend. If I ever need to design a complete lexer, I have a clear picture of what it should look like.
In the future, I plan to tackle some useful extensions like extraction and lookahead (along the lines of Tagged Deterministic Finite Automata with Lookahead).
Going further
To handle UTF-8 and other character encodings, I came to the conclusion that the best approach was to generate the automaton for a fixed encoding (e.g. a normalized form of UTF-8). With a preprocessing step to convert the input. The automaton would still work on an 8-bit alphabet, possibly simulating a single codepoint with multiple transitions.
Out of curiosity, I tried to represent transitions using various forms of packed intervals on which to do binary search. Basically a sorted sequence: (first codepoint, last codepoint, target state). This is a cheap way to handle large alphabets. But I did not manage to make it competitive with the sparse representation, even with clever implementations of binary search like on the excellent PVK's blog. That ruled out the approach for me.